Dekompresní teorie a praxe
Výtah z přednášky ze dne 18.2.1999
Obsah
- Základní pojmy
- Úvod k dekompresnímu modelování
- Odbočka k fyziologii
- Použitá označení veličin
- Základy modelování
- Klasické dekompresní modely
- Bublinové dekompresní modely
- Praktické závěry
- Použité informační zdroje
Tato práce byla původně publikována 2.3.99, v říjnu 2004 prošla lehkou úpravou.
Základní pojmy
Dekompresní postup
Předpis činností, které má potápěč udělat po zahájení výstupu z hloubky "na dně" až po okamžik, kdy nemusí na proběhlý ponor brát ohled. Zahrnuje profil výstupu - dekompresní zastávky a výstupové rychlosti, střídání dekompresních plynů, chování po ponoru. Může ale zahrnovat i další věci - například hydrataci během dekomprese.
Dekompresní algoritmus
Postup stanovení dekompresního postupu. Aby byl použitelný pro plánování ponorů, musí být jednoznačný a úplný. Pro stejné zadání, stejné informace o ponoru a potápěči, musí dávat stejné výsledky.
Dekompresní algoritmus je obvykle založen na dekompresním modelu. Ale může být založen i na souboru předchozích zkušeností, v sofistikované formě označovaném jako statistický model.
Dekompresní algoritmus může být implementován v softwaru pro plánování ponorů - ať už pro stolní počítač, nebo pro počítač potápěčský. Pomocí softwaru mohou být sestavovány tabulky. V historii byly dekompresní algoritmy implementovány i v mechanických, pneumatických a hydraulických zařízeních.
Dekompresní model
Model zobrazující chování lidského těla v prostředí s proměnným vnějším tlakem a případně i proměnnou skladbou dýchacího média s ohledem na vznik dekompresní choroby.
Zpravidla model řeší:
1. sycení těla plyny
2. vysycování plynů z těla, případně změnu fáze plynu v těle (vznik bublin)
3. limity, stanovující minimální přípustný okolní tlak (hloubku).
Matematicky je dekompresní model model obvykle vyjádřen soustavou diferenciálních rovnic.
Tkáň v dekompresním modelu
Diskrétní element, který odděluje a soustřeďuje uvažované vlastnosti určité části kontinua, v simulační teorii se taková entita běžně označuje slovem kompartment.
Tělo tvoří spojitý prostor, kontinuum. Je tvořeno tkáněmi v anatomickém a biologickém významu toho slova. Když se tělo rozloží na obrovské množství malých částí a ty roztřídí do skupin s podobnými vlastnostmi, získá se relativně malý počet (v praxi 8 až 32) virtuálních tkání. Každá z nich má přesně definované vlastnosti, zastupující řekněme průměr dané skupiny.
Nedá se říci, která biologická tkáň patří do které virtuální tkáně v dekompresním modelu. Kousek tam a kousek zase jinam.
Difúze
Pronikání částic (zpravidla molekul) z oblasti vyšší koncentrace do oblasti nižší koncentrace, probíhající do té doby, než se koncentrace vyrovnají. K difúzi dochází v plynech, kapalinách a omezeně i v pevných látkách. U plynů koncentrace odpovídají parciálním tlakům.
Difúzí jsou například transportovány plyny z plic do krve skrz stěnu plicního sklípku.
Perfúze
Transport pohybem média.
Perfúzí jsou například přenášeny plyny rozpuštěné v krvi pomocí krevního oběhu..
Inertní plyn
V dekompresní teorii se za inertní plyny označují plyny, nevstupující za normálních podmínek podstatným způsobem do biochemických reakcí v organismu.
Označení je to poněkud zavádějící, protože některé plyny z této skupiny, zejména dusík, se aktivně účastní mnoha reakcí. Nicméně množství vdechlého a následně fyzikálně rozpuštěného dusíku vstupujícího do chemických reakcí je zanedbatelné.
Explozívní dekomprese
Dekomprese velmi rychlým snížením okolního tlaku, například při neřízeném výstupu nebo při ztrátě těsnosti hyperbarické komory.
HPNS
High pressure nervous syndrome (syndrom z vysokého tlaku) je způsoben tlakem samotným, nikoli chemickým působením plynů. Pravděpodobnou příčinou jsou změny v chování buněčných membrán při vysokém tlaku. HPNS se projevuje v hloubkách, které nemají s rekreačním potápěním nic společného, od 100 až 200 m hlouběji.
Hydrofobie
Vodoodpudivost. Hydrofobní povrch je nesmáčivý, odpuzuje vodu. Hydrofobní může být i kapalina, například olej - potom se s vodou nemísí (nebo mísí jen nesnadno). Opakem je hydrofilie.
Hydrofilie
Hydrofilní povrch je smáčivý. Je-li například z hydrofilního materiálu zhotovena tkanina, je nasákavá (např. bavlna). Ale hydrofilní povrch nasákavý být nemusí, stačí, že je smáčivý, přitahuje vodu. Učebnicová definice je "se zvýšenou afinitou k vodné fázi". Opakem je hydrofobie.
Vasokonstrikce
Zúžení cév.
Úvod k dekompresnímu modelování
"Jestliže dekompresní fyzika a fyziologie může být oprávněně považována za vědu, sestavování dekompresních postupů je více uměním," uvádí Richard D. Vann v knize The Physiology and Medicine of Diving uvádí. Pro exaktní přístup je stále ještě příliš mnoho neznámých.Vývoj každého modelu prochází třemi fázemi:
- Formulace teoretických předpokladů, sestavení modelu a algoritmů,
- Výpočet tabulek,
- Testování v praxi, v případě neúspěšných testů návrat k prvnímu bodu.
Odbočka k fyziologii
Známe primární příčinu dekompresních potíží - je to změna tlaků a změna dýchané směsi plynů. Co ale neznáme zcela přesně, jsou mechanismy vzniku dekompresní choroby. Víme, že za určitých podmínek vznikají v těle bubliny, přesný mechanismus vzniku bublin je však neznámý. Víme, že bubliny v těle způsobují potíže, neumíme však přesně popsat, jaké množství bublin způsobuje potíže. Od chvíle, kdy v roce 1670 Robert Boyle dělal pokusy se zmijí pod vývěvou a všiml si bubliny v jejím oku, však přece jen nějaké poznatky současná věda má.
Efekt zvýšení parciálního tlaku plynů
Takzvaně inertní plyny zasahují za zvýšeného parciálního tlaku do procesů probíhajících v organismu. Krátkodobým projevem jsou zejména jejich narkotické účinky, což je patrně fyzikální jev. Vstupují ale i do biochemických procesů, čímž mění chování organismu dlohodobě.
Kyslík je za vyššího parciálního tlaku toxický, zejména chronická, pulmonární toxicita vede k podstatným změnám na plicích i v celém oběhovém systému, což se pochopitelně projeví i na chování organismu při dekompresi. Více se dočtete v článku Celková otrava kyslíkem.
Efekt zvýšeného hydrostatického tlaku
Hyperbarická expozice předchází z principu každé dekompresi. Tlak samotný zejména způsobuje změny v chování buněčných membrán. Tato změna je jedním z hlavních faktorů vzniku HPNS. Dlouhodobé hyperbarické expozice vyvolávají řadu fyziologických změn, mění se produkce některých hormonů, mění se složení krve. Řada těchto změn neodezní okamžitě se změnou tlaku a má tak vliv na další průběh dekomprese.
Efekt zvýšeného hydrostatického tlaku se jen málo projeví při běžném sportovním potápění, může však být důležitý při potápění v extrémních hloubkách a při potápění saturačním.
Vlivy na sycení a vysycování inertních plynů
Zjednodušeně řečeno, na sycení má vliv tlak, teplota, čas a difúzní a perfúzní charakteristiky tkání. Na vysycování má ještě zásadní vliv vznik bublin. Většina dekompresních modelů si s těmito veličinami vystačí a ostatní vlivy zanedbává.
Mechanické působení bublin
Rozvoj detekčních technik (dopplerův detektor) přispěl k přehodnocení vlivu bublin na dekompresní chorobu. Někdy je prokázáno velké množství bublin bez pozorovatelných příznaků dekompresní choroby, jindy vznikne dekompresní choroba bez přítomnosti zjistitelných bublin. Ucpání cév a mechanické poškození tkání je nejdůležitější příčinou dekompresní choroby po explozívní dekompresi, při neexplozívním průběhu jsou významnější povrchové efekty.
Ucpání cév způsobí zvýšení tlaku, které má za důsledek průnik krevní kapaliny stěnou cévy, čímž dochází ke zmenšení objemu krve v oběhu a zároveň ke zvýšení viskozity. Zvýšená koncentrace částic a látek, způsobující srážení, vede ke zvýšení účinnosti povrchových efektů.
Povrchové efekty bublin
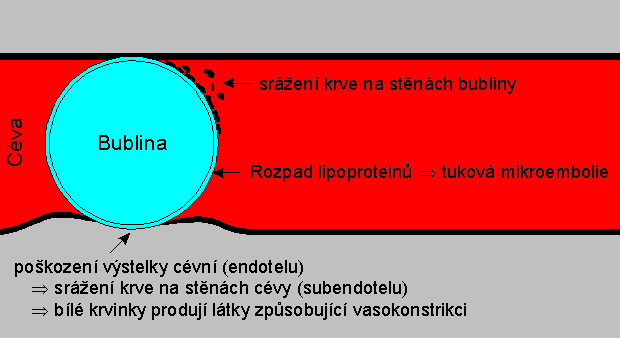
Na rozhraní kapaliny a plynu se odehrává celá řada fyzikálně-chemických dějů. Dlouhé molekuly lipoproteinů přítomných v krvi se otočí svojí hydrofobní částí směrem k plynu a hydrofilní do okolní krve. Na stěně bubliny dojde k vytvoření lipoproteinové vrstvičky. Síly, které způsobují otočení molekul lipoproteinů, jsou tak velké, že dokáží molekuly roztrhnout. Zlomky molekul proteinů se shlukují, zvyšuje se viskozita krve, součástí shluků se stávají červené krvinky a ve výsledku dojde k mikroembolii.
Při rozpadu bílých krvinek, provázejícím srážení krve, se uvolňuje serotonin, který způsobuje vasokonstrikci. Následkem je ještě pevnější sevření bubliny a další poškození cévní výstelky. Spouští se mechanismy, které normálně slouží k zástavě krvácení, zde však místo zástavy krvácení tvoří překážku krevního oběhu.
Použitá označení veličin
| pa | okolní tlak |
| pa min | minimální přípustný okolní tlak (bez symptomů dekompresní nemoci) |
| pi | parciální tlak (není-li uvedeno jinak, rozumí se dusíku) ve vdechovaném médiu |
| pt | parciální tlak v tkání (není-li uvedeno jinak, rozumí se parciální tlak rozpuštěného dusíku) |
| kp | koeficient přesycení |
| T | Časová konstanta |
| Tht | Poločas |
Základy modelování
Sycení jedné tkáně
Nasycení tkáně pt závisí na výchozím nasycení p0, tlaku okolního prostředí pa a času t.
Tak, jako mnoho dalších jevů v přírodě, i jevy difúze a perfúze se dají dobře modelovat pomocí soustavy prvního řádu.
Pro snazší představu si načrtněme hydraulický model.
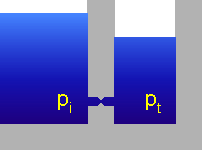
Přechodová charakteristika soustavy popisující průběh nasycení tkáně pt po skokové změně tlaku okolního prostředí pa je na následujícím obrázku.
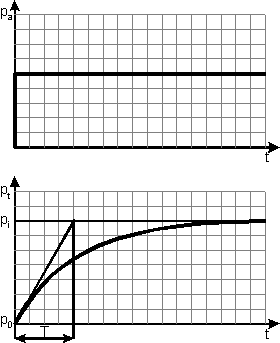
Základní vlastností soustavy prvního řádu je, že její vlastnosti závisí pouze na časové konstantě T. V potápěčské literatuře se častěji než časová konstanta uvádí poločas. Dá se odvodit, že časová konstanta T se dá z poločasu Tht spočítat vydělením přirozeným logaritmem dvojky.
Chování soustavy je popsáno diferenciální rovnicí
která má známé analytické řešení
Vzhledem k poměrně malé rychlosti změn (časová konstanta T je mnohem větší, než možný krok simulace) si můžeme bez velké chyby dovolit použít tu nejjednodušší numerickou metodu - metodu Eulerových polygonů.
Algebraickou úpravou dostaneme
což zapsáno slovně (s malým zjednodušením) znamená
V okolí počátku tedy nahrazujeme křivku její tečnou. Při numerické simulaci se musí zvolit tak malý krok, aby chyba způsobená linearizací byla zanedbatelná.
V prvním kroku simulace dostaneme první bod křivky. Pro výpočet dalšího kroku simulace stačí posunout počátek do tohoto bodu, čímž redukujeme celou úlohu na výpočet "prvního kroku".
Kyslíkové okno
Sycení inertních plynů závisí pouze na jejich parciálních tlacích ve vdechovaném médiu a ve tkáních a difúzních (resp. perfúzních) vlastnostech. V dekompresních modelech je však nutno uvažovat i s biologicky aktivními plyny, především s kyslíkem a oxidem uhličitým.
Tělo při metabolických procesech kyslík spotřebovává a oxid uhličitý produkuje. Při dýchání vzduchu o atmosférickém tlaku velmi rychle dochází ke spotřebování fyzikálně rozpuštěného kyslíku a tělo dále spotřebovává kyslík chemicky vázaný v hemoglobinu. Kyslíkové okno vznikne jako rozdíl parciálního tlaku kyslíku v krvi po průcodu plicemi a poměrně malého a hlavně v podstatě konstantního parciálního tlaku kyslíku potřebného pro přenos z hemoglobinu do tkáně, přičemž se zmenší o vyprodukovaný oxid uhličitý.
Bylo předpovězeno a experimentálně ověřeno (Le Messuier, 1969), že platí rovnice
Při zvyšujícím se parciálním tlaku kyslíku ve vdechované směsi platí tato rovnice do té doby, dokud pro metabolickou spotřebu nestačí fyzikálně rozpuštěný kyslík. Poté se již kyslíkové okno nezvětšuje. Konstanta 12,2 zahrnuje spotřebu kyslíku i produkci oxidu uhličitého, je nutno uvažovat s určitým rozptylem hodnot.
Klasické dekompresní modely
Klasické modely uvažují pouze s plynem rozpuštěným v tkáních. Dekompresní postup je určován podle minimální hloubky, do které může ještě potápěč vystoupit a tato minimální hloubka závisí pouze na míře nasycení tkání.
Haldanův model
Fyziolog J. S. Haldane provedl začátkem dvacátého století řadu experimentů na kozách, které jako experimentální objekt zvolil pro podobnou hmotnost a poměr vody k tuku v těle, jako u člověka. Zjistil, že pro vznik dekompresní nemoci při rychlém výstupu po delší expozici ve stejné "hloubce" (ponory byly simulovány v hyperbarické komoře) je podstatný poměr tlaku "na dně" a tlaku, do kterého je objekt přenesen. Experimentálně určil, že při poměru tlaků 2:1 se neobjeví žádné příznaky.
Zde je třeba zdůraznit, ža Haldane uvažuje vzduch jako jediný plyn. To například znamená, že po dlouhém pobytu v hloubce 30 m (tlak 4 bar) může potápěč bezpečně vystoupit do hloubky 10 m, kde je tlak poloviční (2 bar). Po dostatečně dlouhé době, kdy dojde k ustálení, může pokračovat a z hloubky 10 m vystoupit na hladinu.
Čekat několik hodin na ustálení je nepraktické, proto dalším úkolem bylo stanovit rychlost, s jakou dochází k sycení a vysycování rozpuštěného biologicky inertního plynu. Pro zjednodušení bylo uvažováno, že parciální tlak rozpuštěného inertního plynu v krvi je totožný jako v dýchacím médiu, že tkáně si vyměňují rozpuštěný plyn pouze s krví a nikoli navzájem (oběma směry stejnou rychlostí) a nakonec že v jedné tkáni je v celém jejím objemu parciální tlak rozpuštěného inertního plynu stejný. Na základě těchto zjednodušení bylo již možno snadno formulovat model. Jeho hydraulické přiblížení znázorňuje následující obrázek.

Pro konstrukci modelu, na základě kterého byly sestaveny první dekompresní tabulky (publikováno 1908), si Haldane zvolil 5 tkání, a to s poločasy 5, 10, 20, 40 a 75 minut. Už při jejich konstrukci však Haldane nepoužil výše zmíněný ale nižší. V té době samozřemě ještě neexistovaly počítače, soustava diferenciálních rovnic byla řešena pomocí pneumatického modelu.
Tabulky začala používat britská Royal Navy. Na stejném konceptu byly založeny i tabulky US Navy z roku 1915, sestavené Frenchem a Stlillsonem, které navíc počítaly i s použitím kyslíku pro dekompresi.
Tabulky založené na Haldanově modelu byly velmi úspěšné pro ponory běžné v době jejich vzniku. S vývojem techniky se postupně zvětšovala dosahovaná hloubka a prodlužovaly časy na dně. S rozvojem komerčního potápění se hledaly cesty ke snížení nákladů. Oproti dnes používaným postupům obsahovaly tabulky mnohem delší časy na dekompresních zastávkách pro relativně krátké ponory do středních hloubek a mnohem kratší pro dlouhé ponory do velkých hloubek.
Pro zajímavost dva malé příklady dekompresních postupů (samozřejmě pro potápění se vzduchem) podle původních tabulek. Pro sestup do 30 m na dobu 30 min jsou zastávky 5 min/6 m a 11 min/3 m; pro sestup do 30 m na dobu 120 min je celkový čas výstupu (včetně dekompresních zastávek) 57 minut (podle Bühlmannových tabulek vychází 167 min).
Model US Navy
Haldanův model byl zpřesněn zejména použitím lepší metodiky experimentů. V roce 1937 byly vydány tabulky (Yarbrough), které byly založeny na sadě tkání se stejnými poločasy, ale s jinými přípustnými koeficienty přesycení. Koeficienty přesycení se na rozdíl od haldanova modelu počítají jako poměr parciálního tlaku rozpuštěného dusíku a okolního tlaku.
Pro tkáň s poločasem 5 min byl například povolený koeficient přesycení zvýšen na 4.35, ale pro tkáň s poločasem 75 min byl ponechán koeficient 1.58 (což odpovídá poměru tlaků 2:1, jelikož při tlaku 2 bar je parciální tlak dusíku ve vzduchu 2 × 0.79 = 1.58 bar). Tyto tabulky odstranily zbytečně dlouhé doby dekomprese po krátkých ponorech, ponechaly však beze změny zvýšené riziko po ponorech delších. Van Der Aue uvádí, že po ponoru do 30 m na 85 min jevilo 50 % dobrovolníků příznaky dekompresní nemoci. Jelikož však statisticky silně převládaly krátké ponory, pro něž byly tabulky bezpečné, dlouho přetrvalo klamné zdání bezpečnosti tabulek jako takových.
V roce 1956 byly vydány tabulky (Dwyer, Des Granges aj.), které uvažují se změnou přípustného koeficientu přesycení s hloubkou a hlavně přidávají další tkáň s poločasem 120 min. Tyto tabulky jsou často používány dodnes. Naval Safety Center uvádí v roce 1976 pouze 0.065% výskyt dekompresní choroby při použití těchto tabulek. Soubor tabulek byl dále doplněn o tabulku výjimečných expozic, pro jejichž konstrukci byly do modelu doplněny tkáně s poločasem 160 a 240 minut. Použití této tabulky však nese výrazně vyšší rizika.
Bühlmannův model ZH-L16
Model je na straně sycení principiálně shodný s haldanovým modelem, liší se jen zvolené poločasy tkání. Je použita sada tkání s poločasy sycení dusíkem 5, 8, 12.5, 18.5, 27, 38.3, 54.3, 77, 109, 146, 187, 239, 305, 390, 498, 635 minut.
Zásadní rozdíl oproti haldanovu modelu je ve výpočtu minimálního přípustného okolního tlaku. Bühlmann totiž neuvažuje s prostým koeficientem přesycení, ale s poněkud složitější (i když stále lineární) závislostí.
Je zřejmé, že haldanův model je speciálním případem tohoto modelu, kdy b=1/kp, a=0.
Koeficienty a/b jsou stanoveny pro každou tkáň, jsou různé pro dusík a helium.
Existují různé modifikace tohoto modelu:
- ZH-L16A teoretický model
- ZH-L16B model určený pro sestavování tabulek
- ZH-L16C model určený pro potápěčské počítače
Další modely, například v počítači Aladin používaný ZH-L8 či pro tabulky z roku 1986 použitý ZH-86 používají jiné počty tkání a odlišnosti jsou i v některých dalších parametrech.
Samostatně je třeba zmínit adaptivní model ZH-L8 ADT, použitý v novějších modelech potápěčských počítačů firmy Uwatec Aladin Pro, Aladin Air-X a Aladin Air. Tento model rozšiřuje dříve používaný model ZH-L8 o uvažování vlivu zvýšeného pracovního zatížení (detekce zrychleného dýchání prostřednictvím měření tlaku), vlivu teploty vody a hlavně vzniku bublin při překročení povolené rychlosti výstupu či vynoření nad hloubku dekompresní zsatávky. Matematický popis tohoto algoritmu nebyl dosud zveřejněn, a to ani v nástinu. Z praktických zkušeností s různými výrobními sériemi zmíněných počítačů však lze usuzovat, že se jedná o odborným odhadem zvýšenou bezpečnost při vzniku některých potenciálně rizikových situací.
Workmannův model (M-values)
Workmannn přišel v roce 1965 se zásadním zjednodušením dosavadních modelů - místo čím dál tím víc komplikovaných vzorců sestavit přímo tabulku hodnot, která by pro každou tkáň a pro každou hloubku dekompresní zastávky určovala maximální parciální tlak rozpuštěného inertního plynu, umožňující výstup na další zastávku. Tento tlak byl nazván jako M-value.
Workmannův model má jedinou podstatnou výhodu - dovoluje své přizpůsobení experimentálním výsledkům pouhou změnou příslušných M-values. Vlastnost spočívající v nahrazení některých výpočtů hledáním v tabulce, výhodná pro ručně prováděné výpočty, se s příchodem výkonných počítačů stává spíše nevýhodou. Zásadní nevýhodou Workmannova modelu pro počítačovou simulaci je předem daný maximální rozsah a odstupňování dekompresních zastávek.
Sériový model
V roce 1983 vydal kanadský DCIEM (Defence and Civil Institute of Environmental Medicine) tabulky, založené na teorii, na níž se započali Kidd a Stubbs pracovat roku 1962.
Na rozdíl od haldanova modelu, kde výměna plynů probíhá přímo mezi jednotlivými tkáněmi a okolím (tj. tkáně jsou uspořádány paralelně), zde výměna plynů probíhá mezi sousedními tkáněmi (tj. tkáně jsou uspořádány sériově). Pro lepší názornost si porovnejme obě hydraulická přiblížení:

Tabulky DCIEM, založené na tomto modelu, vydal roku 1994 Svaz potápěčů české republiky. Mezi jejich zajímavosti patří i dekomprese s kyslíkem, prováděná v hloubce 9 m, tj. při překročení "magické" hranice parciálního tlaku kyslíku 1.6 bar.
Jednotkáňový (slab, bulk) model
Model sycení, uvažující difúzi probíhající v objemu. Neuvažuje sycení řady tkání, ale popisuje nasycení v různé vzdálenosti x od rozhraní s okolím.

V hydraulickém přiblížení je možno si představit pronikání do porézní hmoty. Můžeme si také tento model přiblížit jako sériový model s velmi vysokým počtem tkání.
Nasycení je (podle Wienkeho) popsáno rovnicí
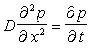
kde D je difúzní koeficient.
Hlavní výhodou modelu je odstranění nutnosti řešení soustavy diferenciálních rovnic a nahrazení rovnicí jedinou. Dnes, v době výkonných počítačů, ztrácí tato výhoda na váze a je spíše nevýhodou - je jednodušší použít hrubou sílu pro řešení více jednoduchých rovnic, než inteligenci pro řešení rovnice jediné, ale značně složité.
Podle tohoto modelu byly sestaveny tabulky BSAC (Hennessy).
Bublinové dekompresní modely
Sycení a vysycování rozpuštěných plynů probíhá stejně, jako u modelů klasických. Bublinový model však navíc počítá se vznikem bublin v těle při vysycování a dekompresní postup určuje podle maximálního množství a velikosti bublin v těle potápěče po ponoru. Malé množství bublin totiž nevadí (mluví se o tzv. tichých bublinách), podle Maikena tělo dokonce i v normálních podmínkách jisté malé množství bublin obsahuje.
V praxi bublinové modely přinášejí oproti modelů klasickým bezpečnější postupy v situacích, kdy dochází k několikanásobné změně hloubky - při opakovaných ponorech, dlouhých sériích ponorů a jo-jo ponorech.
Růst a rozpouštění bubliny probíhá difůzí, jejíž rychlost je dána rozdílem (parciálních) tlaků uvnitř a vně bubliny. Tlakové poměry se dají vyjádřit rovnicí (pro potápění se vzduchem a nitroxem)
kde
PB tlak uvnitř bubliny
PA tlak okolí
PS tlak vyvolaný povrchovým napětím
PE tlak vyvolaný elasticitou tkáně
Tlak uvnitř bubliny závisí na povrchovém napětí a poloměru bubliny
kde
![]() povrchové napětí
povrchové napětí
R poloměr bubliny
Bubliny se rychleji rozpouštějí ve větších hloubkách, kdy je jejich průměr menší a vnitřní přetlak vyvolaný povrchovým napětím větší. Tím je také vysvětlen požadavek hlubších dekompresních zastávek oproti klasickým modelům.
Úzkým místem všech teorií zatím zůstává samotný vznik bubliny. Je známo, že vznik bublin je podpořen kavitací, která vzniká při změně směru proudění kapaliny okolo překážek. Růst bublin usnadňuje i drsný povrch stěn, který díky omezení styčné plochy mezi kapalinou a bublinou omezuje účinky povrchového napětí. Yountovy experimenty nasvědčují tomu, že při vzniku se bubliny chovají, jako kdyby povrchové napětí bylo nulové. Přesný mechanismus není dosud znám.
Varying Permeability Model (VPM)
Model (Yount, Hoffman, později Maiken a Baker) je pojmenován podle polopropustné vrstvy molekul na povrchu bublin, která svoji propustnost pro plyn mění podle tlaku plynů. Dekompresní postup je určován tak, aby nebyl překročen celkový kritický objem plynu ve formě bublin.
VMP má z hlediska simulace tu nepříjemnou vlastnost, že doporučený postup se neodvozuje pouze z minulých stavů, ale i z předpokládaného dalšího postupu. Nelze tedy stanovit dekompresní postup bez toho, aniž by byl naplánován celý profil výstupu. Tato vlastnost nijak zvlášť nevadí na výkonných počítačích, je však omezujícím faktorem pro použití počítačích potápěčských.
Popis VPM je k dispozici pro veřejnost, existuje několik více-méně experimentálních implementací (například V-planner).
Reduced Gradient Bubble Model (RGBM)
Model (Wienke) se vyvinul z výše popsaného VPM. Obdobně je žádaný stav takový, aby množství bublin v těle nepřekročilo určitý kritický objem. Rychlost vzniku bublin závisí na gradientu, který je v tomto modelu definován jako rozdíl mezi parciálním tlakem vdechovaného biologicky inertního plynu a parciálním tlakem plynu rozpuštěného v tkáni (který se počítá podle klasického modelu s tkáněmi s poločasy 1, 2, 5, 10, 20, 40, 80, 120, 240, 480, 720 min.). Model předpokládá, že pro atmosférický tlak platí, že bubliny s poloměrem větším než 0.8 tisícin milimetru rostou a menší se rozpouštějí. Gradient je dále redukován třemi faktory (odtud také pochází název modelu):
- Krátkodobý opakovací faktor
- Faktor, který zohledňuje ponory opakované s velmi krátkým povrchovým intervalem. Tento faktor ovlivňuje výpočet do doby asi dvou hodin po ukončení předchozího ponoru.
- Dlouhodobý opakovací faktor
- Faktor, který zohledňuje opakované ponory v měřítku dní. Tento faktor ovlivňuje výpočet po dobu asi dvou týdnů po předchozím ponoru.
- Faktor reverzního profilu
- Faktor, který zmenšuje přípustný gradient při překročení maximální hloubky předchozího ponoru při opakovaném ponoru.
Úplný popis RGBM je neveřejný, Wienke prodává licenci k jeho užití za velmi vysokou cenu. Plná implementace v komerčním produktu je dostupná v GAPu a ABYSSu.
Některé potápěčské počítače (např. Suunto, Mares, Dacor, ABYSS, HydroSpace, Plexus) mají implementován model který je z marketinových důvodů označováno za "modifikovaný rekreační algoritmus RGBM". Počítač má ve skutečnosti implementován klasický model s M-values, ale ty jsou ovlivňovány výše zmíněnými redukčními faktory. Tyto algoritmy jsou samozřejmě užitečné, ale s "plným" RGBM nemají prakticky nic společného. Podobný počin již dávno udělal Uwatec se svým ADT.
Praktické závěry
Použití jiných plynů a směsí než vzduchu
EAN (Enriched Air Nitrox)
Z dekompresního hlediska je velmi výhodné zvýšit obsah kyslíku. Zvětší se tím kyslíkové okno, což urychluje vysycování dusíku. A jelikož tkáně se sytí dusíkem na základě jeho parciálního tlaku ve směsi, dochází i k menšímu nasycení. Potápění s Nitroxem jako jedinou směsí patří asi budoucnost rekreačního potápění, jelikož pro běžné rekreační hloubkové limity slibuje delší bezdekompresní časy a konec konců, na dražším Nitroxu je větší zisk. Velmi výhodné je použití Nitroxu pro pracovní potápění ve středních hloubkách. Pro potápění se používá zpravidla směs s 30% až 40% kyslíku.
Základní nevýhodou potápění s Nitroxem je jeho vyšší cena oproti vzduchu. Dále je potřeba při plánování ponoru zohlednit toxicitu kyslíku, která při ponorech se vzduchem zpravidla nehraje podstatnou roli. V neposlední řadě je pro přípravu Nitroxu přepouštěním potřeba mít kyslíkově čisté lahve a další techniku mít přizpůsobenou vyšší koncentraci kyslíku ve směsi.
Pro technické potápění se Nitrox používá zejména pro urychlení dekomprese díky kyslíkovému oknu. Běžný postup počítá s použitím trimixu pro pobyt v hloubce, pro dekompresi se v hloubce okolo 20 m přechází na EAN 50 (Nitrox s 50% kyslíku) a na zastávkách v 6 a 3 m se dýchá čistý kyslík.
Směsi s heliem
Helium se používá především pro svůj v podstatě neměřitelný narkotický účinek pod zvýšeným tlakem. Rychlost difúze helia je asi 2.65× rychlejší, než u dusíku. Tato vlastnost jej z dekompresního hlediska znevýhodňuje pro krátké ponory, kdy prodlužuje dobu potřebnou pro výstup. Naopak, pro velmi dlouhé ponory, kdy se stav nasycení blíží saturaci, je použití směsí s heliem z hlediska zkrácení dekompresních časů výhodné. Pro hluboké ponory má helium ještě tu příjemnou vlastnost, že má menší hustotu a tudíž se klesají dechové odpory. Dekompresní nemoc při dýchání helia má zpravidla méně nebezpečný průběh.
Pro pracovní potápění je často používán Heliox, což je směs zpravidla 80% helia a 20% kyslíku. Pro velmi hluboké ponory se pochopitelně obsah kyslíku zmenšuje. Z důvodu ceny a z důvodu prevence vzniku HPNS se používá Trimix, což je směs helia, dusíku a kyslíku. Pro dekompresi se obvykle používá Nitrox a čistý kyslík.
"Jojo" ponory
Podle klasického algoritmu dochází ke zkrácení dekompresních časů při ponorech s pilovitým profilem. Ve skutečnosti se při každém vynoření vytvoří další bubliny, které se při krátkém zanoření nestačí rozpustit a slouží naopak jako jádra pro tvorbu dalších bublin. Výsledkem je vznik dekompresní nemoci i při dodržení limitů daných tabulkami nebo potápěčským počítačem. Bublinové modely toto velmi dobře zohledňují, stejně jako adaptivní model v posledních modelech počítače Aladin.
Jak zvýšit bezpečnost dekompresního postupu
Při rekreačním potápění se často potápěč dostane do situace, kdy zvažuje postup, který by po náročnějším ponoru co nejvíce omezil rizika vzniku dekompresní nemoci.
V první řadě jsou zásady, které je třeba dodržovat vždy:
- Dělat "hladké" ponory - neměnit často a zbytečně hloubku, zejména se vyvarovat plavání nahoru a dolu v malé hloubce po dokončené stupňovité dekompresi. Po dekompresi je v těle určité množství "tichých" bublin, které mohou několikanásobnými změnami tlaku v malé hloubce zvětšit svůj objem nabalením dalších molekul plynů.
- Udržovat dostatek tekutin v těle, doplnění tekutin by mělo být jednou z prvních činností potápěče po vynoření. Při dlouhých ponorech je nutno zajistit rehydrataci i během ponoru. Po opuštění vody je velmi vhodným nápojem "dekompresní" pivo, neboť alkohol i v malém množství přispívá k roztažení cév, cukr pomůže rychle doplnit energii a voda doplní tekutiny. Ovšem nic se nesmí přehnat.
- Po vynoření udržovat tělo v klidu, jakékoli zvýšení tělesné námahy může přivodit problémy. Poslední dekompresní zastávka je vždy na hladině a tak se podle toho je také třeba chovat.
Pro nadstandardní zvýšení bezpečnosti je vhodné:
- Dělat hloubkové bezpečnostní zastávky (deepstops) i při použití dekompresních postupů, které to přímo nevyžadují - což jsou všechny postupy založené na klasických algoritmech, včetně všech současných potápěčských počítačů určených pro rekreační potápění. Postup je podrobně popsán v práci R. L. Pyla.
- Po vynoření setrvat ještě několik minut na hladině. Při výstupu z vody dojte ke změnám v krevním tlaku v různých částech těla, což vyvolá přesuny krve a může vést k lokálnímu snížení tlaku v horních partiích těla na takovou úroveň, která způsobí vznik bublin. Patrně nebyl ještě proveden žádný seriózní výzkum na toto téma, ale řada technických potápěčů tvrdí, že příznaky dekompresní choroby se zpravidla neprojeví ani při několikahodinové dekompresi, ale běžně už za 20-30 minut po vynoření.
- Při použití potápěčského počítače dělat zastávky v o trochu větší hloubce, než počítač předepisuje. Zejména se to týká ponorů, kdy je potřeba vykonat několik zastávek. Samozřejmě tím dojde k prodloužení celkové doby výstupu.
- V případě postupu podle tabulek je zpravidla postup určen metodikou, tabulky doprovázející. Obvykle se bere o jeden řádek vyšší hloubka, než odpovídá hloubce skutečné.
Řešení krizových situací
Dekompresní tabulky obvykle udávají metodiku řešení opomenuté dekomprese.
Co však dělat, když potápěč v průběhu ponoru zjistí, že nemá dostatek vzduchu na provedení řádné dekomprese, přičemž nemá na hladině žádnou záložní láhev, aby mohl celý problém řešit postupem pro opomenutou dekompresi? Tady je každá rada drahá a vůbec nepomůže obvyklé mentorování, že prostě musí mít na člunu nebo na břehu nějakou zálohu.
Některé zásady pro minimalizaci rizika vzniku závažných následků při různých nehodách:
- Jestliže ukazuje potápěčský počítač spustil alarm, signalizující nulový RBT (remaining bottom time - zbývající čas na dně), nepropadejte panice. Počítač uvažuje s rezervou v lahvi a právě pro řešení problémů tam ta rezerva je. Je samozřejmě potřeba bez zbytečného otálení zahájit výstup, ovšem je-li například na vraku výstupové lano vzdálené asi 50 m, je pořád dost času k němu doplavat.
- Jestliže jeden z dvojice nemá dostatek vzduchu pro celý výstup, ale jeho buddy ano, pak je vždy lepší dýchat ve dvou na hlubších zastávkách a nečekat, až vzduch opravdu dojde. Ve větší hloubce je větší spotřeba a na poslední zastávce ve 3 m bývají často vlny. Také může být potřeba z nějakého důvodu se na chvíli oddělit.
- Jestliže dvojice nemá dostatek vzduchu na řádné provedení celého dekompresního postupu podle Bühlmannova algoritmu (tedy například podle tabulek vydaných SPČR nebo podle počítače Uwatec Aladin), není opět třeba propadat panice. Pro tento účel je vhodné znát (nebo mít na vhodném místě poznamenaný) postup podle tabulek US Navy (staré svazarmovské), které dovolují znatelně rychlejší dekompresi a dají se tedy dobře použít jako tabulky pro řešení nouzových situací.
- Když už dojde k porušení dekompresního postupu, nejsou patrné žádné příznaky (nebo jen bolestivé) a je k dispozici zkušený potápěč a další zdroj vzduchu (či lépe kyslíku), je možné udělat náhradní rekompresi ve vodě podle některé z metodik. Dýchání kyslíku a převoz do komory je samozřejmě nejlepší řešení v případě, kdy je komora na blízku, proto také DAN (Divers Alert Network) rekompresi ve vodě výslovně nedoporučuje.
- Po dekompresní nehodě, i když je bez příznaků dekompresní nemoci, je třeba důkladně doplnit tekutiny, tentokrát pokud možno bez alkoholu. Čím více tekutin do sebe dokáže postižený potápěč vpravit, tím lépe. Je vhodné podat jednu tabletu Aspirinu, který působí proti srážení krve. Není však dobré podávat Aspirin preventivně, protože snížení srážlivosti krve může mít fatální důsledky v případech krvácení. Ani v případě bolestivých projevů dekompresní nemoci I. typu (bends) by neměly být podávány utišující prostředky, protože by to velmi ztížilo lékařskou diagnózu. Postižený by měl několik hodin v klidu ležet.
Použité informační zdroje
- Balda, Hanuš, Základy technické kybernetiky, SNTL 1986
- Bennett, Elliott, The Physiology and Medicine of Diving, Baillire Tindall 1982
- Bookspan, Diving Physiology In Plain English, UHMS 1995
- Bühlmann, Tauchmedizin, Springer 1995
- Maiken, Bubble Decompression Strategies, přednáška na konferenci tek95 (zdroj Internet)
- Novomeský František, videozáznam z přednášky 1998
- Pyle, The importance of Deep Safety Stops, přednáška na DeepTech (zdroj překlad na Stranách potápěčských)
- Silbernagl, Despopoulos, Atlas fyziologie člověka, Grada Avicenum 1993
- Technický naučný slovník, SNTL 1.díl 1981 až 7. díl 1986
- Wienke, Basic Diving Physics And Applications, Best Publishing Co. 1994
- Wienke, Decompression Models And Phase Mechanics, Los Alamos National Laboratory (zdroj Internet)
- Yount, Hoffman, On the Use of a Bubble Formation Model to Calculate Diving Tables. Aviation, Space, and Environmental Medicine, February, 1986 (zdroj Internet)
- Zítek, Simulace dynamických systémů, SNTL 1990
